Complex Number Multiplication

A Complex Number is a combination of a Real Number and an Imaginary Number:

A Real Number is the type of number we use every day.

Examples: 12.38, ½, 0, −2000

An Imaginary Number, when squared gives a negative result:

imaginary squared gives negative

The "unit" imaginary number when squared equals −1

i² = −1

Examples: 5i, −3.6i, i/2, 500i

Examples of Complex Numbers:

3.6 + 4i		(real part is 3.6, imaginary part is 4i)
−0.02 + 1.2i		(real part is −0.02, imaginary part is 1.2i)
25 − 0.3i		(real part is 25, imaginary part is −0.3i)

Either part can be zero:

0 + 2i		(no real part, imaginary part is 2i)		same as 2i
4 + 0i		(real part is 4, no imaginary part)		same as 4

Multiplying

To multiply complex numbers:

Each part of the first complex number gets multiplied by
each part of the second complex number

Just use "FOIL", which stands for "Firsts, Outers, Inners, Lasts" (see Binomial Multiplication for more details):

	Firsts: a × c Outers: a × di Inners: bi × c Lasts: bi × di
(a+bi)(c+di) = ac + adi + bci + bdi²

Like this:

Example: (3 + 2i)(1 + 7i)

(3 + 2i)(1 + 7i) = 3×1 + 3×7i + 2i×1+ 2i×7i

= 3 + 21i + 2i + 14i²

= 3 + 21i + 2i − 14 (because i² = −1)

= −11 + 23i

Here is another example:

Example: (1 + i)²

(1 + i)²= (1 + i)(1 + i)

= 1×1 + 1×i + 1×i + i²

= 1 + 2i − 1 (because i² = −1)

= 0 + 2i

But There is a Quicker Way!

Use this rule:

(a+bi)(c+di) = (ac−bd) + (ad+bc)i

Example:

(3 + 2i)(1 + 7i) = (3×1 − 2×7) + (3×7 + 2×1)i

= −11 + 23i

Why Does That Rule Work?

It is just the "FOIL" method after a little work:

(a+bi)(c+di)	=	ac + adi + bci + bdi²	FOIL method
	=	ac + adi + bci − bd	(because i²=−1)
	=	(ac − bd) + (ad + bc)i	(gathering like terms)

And there you have the (ac − bd) + (ad + bc)i pattern.

This rule is certainly faster, but if you forget it, just remember the FOIL method.

Now let's see what multiplication looks like on the Complex Plane.

The Complex Plane

This is the complex plane:

complex plane

It is a plane for complex numbers!

We can plot a complex number like 3 + 4i :

It is placed

3 units along (the real axis),
and 4 units up (the imaginary axis).

Multiplying By i

Let's multiply it by i:

(3 + 4i) x i = 3i + 4i²

Which simplifies to (because i² = −1):

−4 + 3i

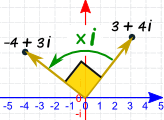And here is the cool thing ... it's the same as rotating by a right angle (90° or π/2)

Was that just a weird coincidence?

Let's try multiplying by i again:

(−4 + 3i) x i = −4i + 3i² = −3 − 4i

and again:

(−3 − 4i) x i = −3i − 4i² = 4 − 3i

and again:

(4 − 3i) x i = 4i − 3i² = 3 + 4i

complex plane vector by i 4 times is full rotation

Well, isn't that stunning? Each time it rotates by a right angle, until it ends up where it started.

Let's try it on the number 1:

1 × i		= i
i × i		= −1
−1 × i		= −i
−i × i		= 1
Back to 1 again!

Each time a right angle rotation.

Choose your own complex number and try that for yourself, it is good practice.

Let's look more closely at angles now.

Polar Form

Our friendly complex number 3 + 4i :

Here it is again, but

in polar form:
(distance and angle)

So the complex number 3 + 4i can also be shown as distance (5) and angle (0.927 radians).

How do we do the conversions?

Example: the number 3 + 4i

We can do a Cartesian to Polar conversion:

r = √(x² + y²) = √(3² + 4²) = √25 = 5
θ = tan^-1 (y/x) = tan^-1 (4/3) = 0.927 (to 3 decimals)

We can also take Polar coordinates and convert them to Cartesian coordinates:

x = r × cos( θ ) = 5 × cos( 0.927 ) = 5 × 0.6002... = 3 (close enough)
y = r × sin( θ ) = 5 × sin( 0.927 ) = 5 × 0.7998... = 4 (close enough)

In fact, a common way to write a complex number in Polar form is

x + iy	=	r cos θ + i r sin θ
	=	r(cos θ + i sin θ)

And "cos θ + i sin θ" is often shortened to "cis θ", so:

x + iy = r cis θ

cis is just shorthand for cos θ + i sin θ

So we can write:

3 + 4i = 5 cis 0.927

In some subjects, like electronics, "cis" is used a lot!

Now For Some More Multiplication

Let's try another multiplication:

Example: Multiply 1+i by 3+i

(1+i) (3+i) =1(3+i) + i(3+i)

=3 + i + 3i + i²

=3 + 4i − 1

=2 + 4i

And here is the result on the Complex Plane:

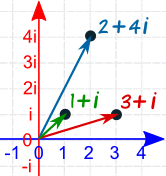
complex plane 1+i, 3+i, 2+4i

But it is more interesting to see those numbers in Polar Form:

Example: (continued)

Convert 1+i to Polar:

r = √(1² + 1²) = √2
θ = tan^-1 (1/1) = 0.785 (to 3 decimals)

Convert 3+i to Polar:

r = √(3² + 1²) = √10
θ = tan^-1 (1/3) = 0.322 (to 3 decimals)

Convert 2+4i to Polar:

r = √(2² + 4²) = √20
θ = tan^-1 (4/2) = 1.107 (to 3 decimals)

Have a look at the r values for a minute. Are they related somehow?
And what about the θ values?

Here is that multiplication in one line (using "cis"):

(√2 cis 0.785) × (√10 cis 0.322) = √20 cis 1.107

This is the interesting thing:

√2 x √10 = √20
0.785 + 0.322 = 1.107

So:

The magnitudes get multiplied.
And the angles get added.

When multiplying in Polar Form: multiply the magnitudes, add the angles.

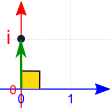
complex plane i is right angle

And that is why multiplying by i rotates by a right angle:

i has a magnitude of 1 and forms a right angle on the complex plane

Squaring

To square a complex number, multiply it by itself:

multiply the magnitudes: magnitude × magnitude = magnitude²
add the angles: angle + angle = 2 , so we double them.

Result: square the magnitudes, double the angle.

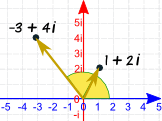
complex plane vector 1+2i squared is -3+4i

Example: Let us square 1 + 2i:

(1 + 2i)(1 + 2i) = 1 + 4i + 4i² = −3 + 4i

On the diagram the angle looks to be (and is!) doubled.

Also:

The magnitude of (1+2i) = √(1² + 2²) = √5
The magnitude of (−3+4i) = √(3² + 4²) = √25 = 5

So the magnitude got squared, too.

In general, a complex number like:

r(cos θ + i sin θ)

When squared becomes:

r²(cos 2θ + i sin 2θ)

(the magnitude r gets squared and the angle θ gets doubled.)

Or in the shorter "cis" notation:

(r cis θ)² = r² cis 2θ

de moivre

De Moivre's Formula

And the mathematician Abraham de Moivre found it works for any integer exponent n:

[ r(cos θ + i sin θ) ]ⁿ = rⁿ(cos nθ + i sin nθ)

(the magnitude becomes rⁿ the angle becomes nθ.)

Or in the shorter "cis" notation:

(r cis θ)ⁿ = rⁿ cis nθ

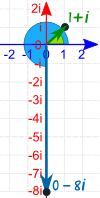
complex plane 0-8i

Example: What is (1+i)⁶