Function Graph

x y graph
An example of a function graph

How to Draw a Function Graph

First, start with a blank graph like this. It has x-values going left-to-right, and y-values going bottom-to-top:

x y graph
The x-axis and y-axis cross over
where x and y are both zero.

Plotting Points

A simple (but not perfect) approach is to calculate the function at some points and then plot them.

A function graph is the set of points of the values taken by the function.

Example: y = x2 − 5

Let us calculate some points:

x y = x2−5
−2 −1
0 −5
1 −4
3 4

And plot them like this:

x y graph

Not very helpful yet. Let us add some more points:

x y graph

Looking better!

We can now guess that plotting all the points will look like this:

x y graph

A nice parabola.

 

We should try to plot enough points to be confident in what is going on!

Example: y = x3 − 5x

With these calculated points:

x y = x3−5x
−2 2
0 0
2 −2

We might think this is the graph:

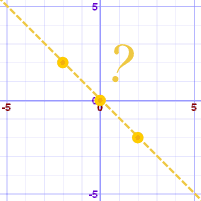
graph

But this is the real graph:

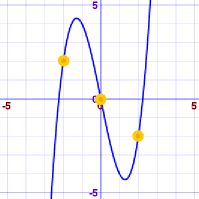
graph

So "plotting some points" is useful, but can lead to mistakes.

Complete Graph

For a graph to be "complete" we need to show all the important features:

This often means thinking carefully about the function.

Example: (x−1)/(x2−9)

On the page Rational Expressions we do some work to discover that the function:

  • crosses the x-axis at 1,
  • crosses the y-axis at 1/9,
  • has vertical asymptotes (where it heads towards minus/plus infinity) at −3 and +3

The result is that we can make this sketch:

function local minimum and maximum
Sketch of (x−1)/(x2−9) from Rational Expressions.

 

Using Calculus

We can also find Maxima and Minima using derivatives :

function local minimum and maximum

Tools to Help You

  • The Function Grapher can help you. Enter the equation as "y=(some function of x)". You can use zoom to find important points.
  • If you can't write the equation as "y=(some function of x)", you can try the Equation Grapher, where you enter equations like "x^2+y^2=9" (meaning x2+y2=9).

But remember they are just a help! They are only computer programs, and could easily miss some important thing on the graph, or not plot something correctly.


Note: you may hear the phrase "satisfy the equation", which means where the equation is true.


 
Algebra Index Data Index