Difference of Two Cubes

There is a special case when multiplying polynomials that produces this: a³ − b³

Polynomials

A polynomial looks like this:

Difference of Two Cubes

The Difference of Two Cubes is a special case of multiplying polynomials :

It comes up sometimes when solving things, so is worth remembering.

And this is why it works out so simply (press play):

Example from Geometry:

Take two cubes of lengths x and y:

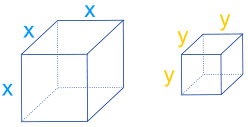
The larger "x" cube can be split into four smaller boxes (cuboids), with box A being a cube of size "y":

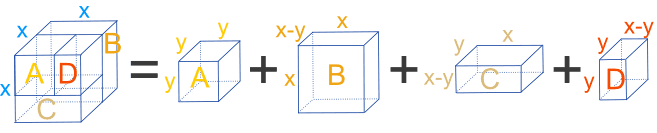
The volumes of these boxes are:

• A = y³
• B = x²(x − y)
• C = xy(x − y)
• D = y²(x − y)

But together, A, B, C and D make up the larger cube that has volume x³:

x3	=	y3 + x2(x − y) + xy(x − y) + y2(x − y)
x3 − y3	=	x2(x − y) + xy(x − y) + y2(x − y)
x3 − y3	=	(x − y)(x2 + xy + y2)

Hey! We ended up with the same formula! Thank goodness.

Sum of Two Cubes

There is also the "Sum of Two Cubes"

By changing the sign of b in each case we get:

(note the minus in front of "ab" also)