Pythagorean Theorem Algebra Proof

What is the Pythagorean Theorem?

You can learn all about the Pythagorean Theorem, but here is a quick summary:

triangle abc

The Pythagorean Theorem says that, in a right triangle, the square of a (which is a×a, and is written a²) plus the square of b (b²) is equal to the square of c (c²):

a² + b² = c²

Proof of the Pythagorean Theorem using Algebra

We can show that a² + b² = c² using Algebra

Take a look at this diagram ... it has that "abc" triangle in it (four of them actually):

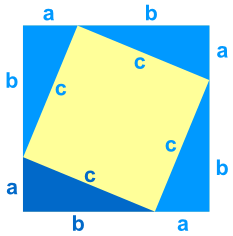
Area of Whole Square

It is a big square, with each side having a length of a+b, so the total area is:

A = (a+b)(a+b)

Area of The Pieces

Now let's add up the areas of all the smaller pieces:

First, the smaller (tilted) square has an area of: c²

Each of the four triangles has an area of:ab2

So all four of them together is:4ab2 = 2ab

Adding up the tilted square and the 4 triangles gives:A = c² + 2ab

Both Areas Must Be Equal

The area of the large square is equal to the area of the tilted square and the 4 triangles. This can be written as:

(a+b)(a+b) = c² + 2ab

NOW, let us rearrange this to see if we can get the pythagoras theorem:

Start with:(a+b)(a+b) = c² + 2ab

Expand (a+b)(a+b):a² + 2ab + b² = c² + 2ab

Subtract "2ab" from both sides:a² + b² = c²

DONE!

Now we can see why the Pythagorean Theorem works ... and it is actually a proof of the Pythagorean Theorem.

This proof came from China over 2000 years ago!

There are many more proofs of the Pythagorean theorem, but this one works nicely.