Real World Examples of
Quadratic Equations
A Quadratic Equation looks like this:
Quadratic equations pop up in many real world situations!
Here we have collected some examples for you, and solve each using different methods:
- Factoring Quadratics
- Completing the Square
- Graphing Quadratic Equations
- The Quadratic Formula
- Online Quadratic Equation Solver
Each example follows three general stages:
- Take the real world description and make some equations
- Solve!
- Use your common sense to interpret the results

Balls, Arrows, Missiles and Stones
When you throw a ball (or shoot an arrow, fire a missile or throw a stone) it goes up into the air, slowing as it travels, then comes down again faster and faster ...
... and a Quadratic Equation tells you its position at all times!
Example: Throwing a Ball
A ball is thrown straight up, from 3 m above the ground, with a velocity of 14 m/s. When does it hit the ground?
Ignoring air resistance, we can work out its height by adding up these three things:
(Note: t is time in seconds)
| The height starts at 3 m: | 3 | |
| It travels upwards at 14 meters per second (14 m/s): | 14t | |
| Gravity pulls it down, changing its position by about 5 m per second squared: | −5t2 | |
| (Note for the enthusiastic: the -5t2 is simplified from -(½)at2 with a=9.8 m/s2) |
Add them up and the height h at any time t is:
h = 3 + 14t − 5t2
And the ball will hit the ground when the height is zero:
3 + 14t − 5t2 = 0
Which is a Quadratic Equation !
In "Standard Form" it looks like:
−5t2 + 14t + 3 = 0
It looks even better when we multiply all terms by −1:
5t2 − 14t − 3 = 0
Let us solve it ...
There are many ways to solve it, here we will factor it using the "Find two numbers that multiply to give a×c, and add to give b" method in Factoring Quadratics:
a×c = −15, and b = −14.
The factors of −15 are: −15, −5, −3, −1, 1, 3, 5, 15
By trying a few combinations we find that −15 and 1 work (−15×1 = −15, and −15+1 = −14)
The "t = −0.2" is a negative time, impossible in our case.
The "t = 3" is the answer we want:
The ball hits the ground after 3 seconds!
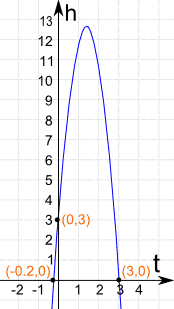
Here is the graph of the Parabola h = −5t2 + 14t + 3
It shows you the height of the ball vs time
Some interesting points:
(0,3) When t=0 (at the start) the ball is at 3 m
(−0.2,0) says that −0.2 seconds BEFORE we threw the ball it was at ground level. This never happened! So our common sense says to ignore it.
(3,0) says that at 3 seconds the ball is at ground level.
Also notice that the ball goes nearly 13 meters high.
Note: You can find exactly where the top point is!
The method is explained in Graphing Quadratic Equations, and has two steps:
Find where (along the horizontal axis) the top occurs using −b/2a:
- t = −b/2a = −(−14)/(2 × 5) = 14/10 = 1.4 seconds
Then find the height using that value (1.4)
- h = −5t2 + 14t + 3 = −5(1.4)2 + 14 × 1.4 + 3 = 12.8 meters
So the ball reaches the highest point of 12.8 meters after 1.4 seconds.
 |
Example: New Sports BikeYou have designed a new style of sports bicycle! Now you want to make lots of them and sell them for profit. |
Your costs are going to be:
- $700,000 for manufacturing set-up costs, advertising, etc
- $110 to make each bike
Based on similar bikes, you can expect sales to follow this "Demand Curve":
- Unit Sales = 70,000 − 200P
Where "P" is the price.
For example, if you set the price:
- at $0, you just give away 70,000 bikes
- at $350, you won't sell any bikes at all
- at $300 you might sell 70,000 − 200×300 = 10,000 bikes
So ... what is the best price? And how many should you make?
Let us make some equations!
How many you sell depends on price, so use "P" for Price as the variable
- Unit Sales = 70,000 − 200P
- Sales in Dollars = Units × Price = (70,000 − 200P) × P = 70,000P − 200P2
- Costs = 700,000 + 110 x (70,000 − 200P) = 700,000 + 7,700,000 − 22,000P = 8,400,000 − 22,000P
- Profit = Sales-Costs = 70,000P − 200P2 − (8,400,000 − 22,000P) = −200P2 + 92,000P − 8,400,000
Profit = −200P2 + 92,000P − 8,400,000
Yes, a Quadratic Equation. Let us solve this one by Completing the Square.
Solve: −200P2 + 92,000P − 8,400,000 = 0
Step 1 Divide all terms by -200
Step 2 Move the number term to the right side of the equation:
Step 3 Complete the square on the left side of the equation and balance this by adding the same number to the right side of the equation:
(b/2)2 = (−460/2)2 = (−230)2 = 52900
Step 4 Take the square root on both sides of the equation:
Step 5 Subtract (-230) from both sides (in other words, add 230):
What does that tell us? It says that the profit is ZERO when the Price is $126 or $334
But we want to know the maximum profit, don't we?
It is exactly half way in-between! At $230
And here is the graph:
Profit = −200P2 + 92,000P − 8,400,000
The best sale price is $230, and you can expect:
- Unit Sales = 70,000 − 200 x 230 = 24,000
- Sales in Dollars = $230 x 24,000 = $5,520,000
- Costs = 700,000 + $110 x 24,000 = $3,340,000
- Profit = $5,520,000 − $3,340,000 = $2,180,000
A very profitable venture.
Example: Small Steel Frame
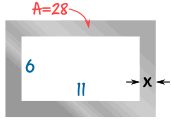
Your company is going to make frames as part of a new product they are launching.
The frame will be cut out of a piece of steel, and to keep the weight down, the final area should be 28 cm2
The inside of the frame has to be 11 cm by 6 cm
What should the width x of the metal be?
Area of steel before cutting:
Area of steel after cutting out the 11 × 6 middle:
Let us solve this one graphically!
Here is the graph of 4x2 + 34x :
The desired area of 28 is shown as a horizontal line.
The area equals 28 cm2 when:
x is about −9.3 or 0.8
The negative value of x make no sense, so the answer is:
x = 0.8 cm (approx.)
Example: River Cruise
A 3 hour river cruise goes 15 km upstream and then back again. The river has a current of 2 km an hour. What is the boat's speed and how long was the upstream journey?
There are two speeds to think about: the speed the boat makes in the water, and the speed relative to the land:
- Let x = the boat's speed in the water (km/h)
- Let v = the speed relative to the land (km/h)
Because the river flows downstream at 2 km/h:
- when going upstream, v = x−2 (its speed is reduced by 2 km/h)
- when going downstream, v = x+2 (its speed is increased by 2 km/h)
We can turn those speeds into times using:
time = distance / speed
(to travel 8 km at 4 km/h takes 8/4 = 2 hours, right?)
And we know the total time is 3 hours:
total time = time upstream + time downstream = 3 hours
Put all that together:
total time = 15/(x−2) + 15/(x+2) = 3 hours
Now we use our algebra skills to solve for "x".
First, get rid of the fractions by multiplying through by (x-2)(x+2):
3(x-2)(x+2) = 15(x+2) + 15(x-2)
Expand everything:
3(x2−4) = 15x+30 + 15x−30
Bring everything to the left and simplify:
3x2 − 30x − 12 = 0
It is a Quadratic Equation! Let us solve it using the Quadratic Formula:
Where a, b and c are
from the
Quadratic Equation in "Standard Form": ax2 + bx + c = 0
Solve 3x2 - 30x - 12 = 0
Answer: x = −0.39 or 10.39 (to 2 decimal places)
x = −0.39 makes no sense for this real world question, but x = 10.39 is just perfect!
Answer: Boat's Speed = 10.39 km/h (to 2 decimal places)
And so the upstream journey = 15 / (10.39−2) = 1.79 hours = 1 hour 47min
And the downstream journey = 15 / (10.39+2) = 1.21 hours = 1 hour 13min
Example: Resistors In Parallel
Two resistors are in parallel, like in this diagram:
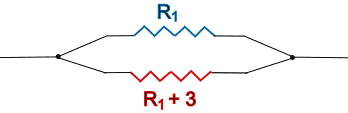
The total resistance has been measured at 2 Ohms, and one of the resistors is known to be 3 ohms more than the other.
What are the values of the two resistors?
The formula to work out total resistance "RT" is:
1RT = 1R1 + 1R2
In this case, we have RT = 2 and R2 = R1 + 3
1 2 = 1 R1 + 1 R1+3
To get rid of the fractions we can multiply all terms by 2R1(R1 + 3) and then simplify:
Yes! A Quadratic Equation !
Let us solve it using our Quadratic Equation Solver.
- Enter 1, −1 and −6
- And you should get the answers −2 and 3
R1 cannot be negative, so R1 = 3 Ohms is the answer.
The two resistors are 3 ohms and 6 ohms.
Others
Quadratic Equations are useful in many other areas:

For a parabolic mirror, a reflecting telescope or a satellite dish, the shape is defined by a quadratic equation.
Quadratic equations are also needed when studying lenses and curved mirrors.
And many questions involving time, distance and speed need quadratic equations.