Scalars and Vectors

(... and Matrices)

What are Scalars and Vectors?

And watch out for these special words:

Distance vs Displacement

• Distance is a scalar ("3 km")
• Displacement is a vector ("3 km Southeast")

You can walk a long distance, but your displacement may be small (or zero if you return to the start).

Speed vs Velocity

• Speed is how fast something moves.
• Velocity is speed with a direction.

Saying Ariel the Dog runs at 9 km/h (kilometers per hour) is a speed.

But saying he runs 9 km/h Westwards is a velocity.

See Speed and Velocity to learn more.

Notation

A vector is often written in bold, like a or b so we know it is not a scalar:

• so c is a vector, it has magnitude and direction
• but c is a scalar, like 3 or 12.4

A vector can also be written as the letters of its head and tail with an arrow above it, like this:

Using Scalars

Scalars are easy to use. Just treat them as normal numbers.

Using Vectors

The page on vectors has more detail, but here is a quick summary:

We can add two vectors by joining them head-to-tail:

We can subtract one vector from another:

• first we reverse the direction of the vector we want to subtract,
• then add them as usual:

a − b

We can multiply a vector by a scalar (called "scaling" a vector):

Example: multiply the vector m = (7,3) by the scalar 3

a = 3m = (3×7,3×3) = (21,9)

It still points in the same direction, but is 3 times longer

(And now you know why numbers are called "scalars", because they "scale" the vector up or down.)

Polar or Cartesian

A vector can be in:

• magnitude and direction (Polar) form,
• or in x and y (Cartesian) form

Like this:

	<=>
Vector a in Polar Coordinates		Vector a in Cartesian Coordinates

(Read how to convert them at Polar and Cartesian Coordinates.)

Have a try of the Vector Calculator to get a feel for how it all works.

Multiplying a Vector by a Vector (Dot Product and Cross Product)

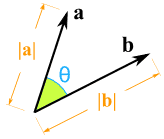How do we multiply two vectors together? There is more than one way! The scalar or Dot Product (the result is a scalar). The vector or Cross Product (the result is a vector). (Read those pages for more details.)

More Than 2 Dimensions

Vectors also work perfectly well in 3 or more dimensions:

The vector (1,4,5)

List of Numbers

So a vector can be thought of as a list numbers:

• 2 numbers for 2D space, such as (4,7)
• 3 numbers for 3D space, such as (1,4,5)
• etc