Separation of Variables

Separation of Variables is a special method to solve some Differential Equations

A Differential Equation is an equation with a function and one or more of its derivatives:

dy/dx = 5xy
Example: an equation with the function y and its derivative dy dx

When Can I Use it?

Separation of Variables: dy/dx = 5xy becomes dy/y = 5x dx

Separation of Variables can be used when:

All the y terms (including dy) can be moved to one side of the equation, and

All the x terms (including dx) to the other side.

Method

Three Steps:

Step 1 Move all the y terms (including dy) to one side of the equation and all the x terms (including dx) to the other side.
Step 2 Integrate one side with respect to y and the other side with respect to x. Don't forget "+ C" (the constant of integration).
Step 3 Simplify

Example: Solve this (k is a constant):

dy dx = ky

Step 1 Separate the variables by moving all the y terms to one side of the equation and all the x terms to the other side:

Multiply both sides by dx: dy = ky dx

Divide both sides by y: dy y = k dx

Step 2 Integrate both sides of the equation separately:

Put the integral sign in front:∫ dy y = ∫ k dx

Integrate left side: ln(y) + C = ∫ k dx

Integrate right side: ln(y) + C = kx + D

C is the constant of integration. And we use D for the other, as it is a different constant.

Step 3 Simplify:

We can roll the two constants into one (a=D−C): ln(y) = kx + a

e^(ln(y)) = y , so let's take exponents on both sides:y = e^{kx + a}

And e^{kx + a} = e^kx e^a so we get:y = e^kx e^a

e^a is just a constant so we replace it with c:y = ce^kx

We have solved it:

y = ce^kx

This is a general type of first order differential equation which turns up in all sorts of unexpected places in real world examples.

We used y and x, but the same method works for other variable names, like this:

rabbits

Example: Rabbits!

The more rabbits you have the more baby rabbits you will get. Then those rabbits grow up and have babies too! The population will grow faster and faster.

The important parts of this are:

the population N at any time t
the growth rate r
the population's rate of change dN dt

The rate of change at any time equals the growth rate times the population:

dN dt = rN

But hey! This is the same as the equation we just solved! It just has different letters:

N instead of y
t instead of x
r instead of k

So we can jump to a solution:

N = ce^rt

And here is an example, the graph of N = 0.3e^2t:

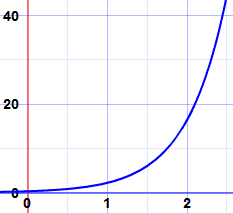
Exponential Growth

There are other equations that follow this pattern such as continuous compound interest.

More Examples

OK, on to some different examples of separating the variables:

Example: Solve this:

dydx = 1y

Step 1 Separate the variables by moving all the y terms to one side of the equation and all the x terms to the other side:

Multiply both sides by dx:dy = (1/y) dx

Multiply both sides by y: y dy = dx

Step 2 Integrate both sides of the equation separately:

Put the integral sign in front:∫ y dy = ∫ dx

Integrate each side: (y²)/2 = x + C

We integrated both sides in the one line.

We also used a shortcut of just one constant of integration C. This is perfectly OK as we could have +D on one, +E on the other and just say that C = E−D.

Step 3 Simplify:

Multiply both sides by 2: y² = 2(x + C)

Square root of both sides:y = ±√(2(x + C))

Note: This is not the same as y = √(2x) + C, because the C was added before we took the square root. This happens a lot with differential equations. We cannot just add the C at the end of the process. It is added when doing the integration.

We have solved it:

y = ±√(2(x + C))

A harder example:

Example: Solve this:

dydx = 2xy1+x²

Step 1 Separate the variables:

Multiply both sides by dx, divide both sides by y:

1y dy = 2x1+x²dx

Step 2 Integrate both sides of the equation separately:

∫1y dy = ∫2x1+x²dx

The left side is a simple logarithm, the right side can be integrated using substitution:

Let u = 1 + x², so du = 2x dx:∫1y dy = ∫1udu

Integrate:ln(y) = ln(u) + C

Then we make C = ln(k):ln(y) = ln(u) + ln(k)

So we can get this:y = uk

Now put u = 1 + x² back again:y = k(1 + x²)

Step 3 Simplify:

It is already as simple as can be. We have solved it:

y = k(1 + x²)

An even harder example: the famous Verhulst Equation

rabbits

Example: Rabbits Again!

Remember our growth Differential Equation:

dNdt = rN

Well, that growth can't go on forever as they will soon run out of available food.

A guy called Verhulst included k (the maximum population the food can support) to get:

dNdt = rN(1−N/k)

The Verhulst Equation

Can this be solved?

Yes, with the help of one trick ...

Step 1 Separate the variables:

Multiply both sides by dt: dN = rN(1−N/k) dt

Divide both sides by N(1-N/k):1N(1−N/k)dN = r dt

Step 2 Integrate:

∫1N(1−N/k)dN = ∫ r dt

Hmmm... the left side looks hard to integrate. In fact it can be done with a little trick from Partial Fractions ... we rearrange it like this:

We start with this:1N(1−N/k)

Multiply top and bottom by k:kN(k−N)

Now here is the trick, add N and −N to the top:N+k−NN(k−N)

and split it into two fractions:NN(k−N) + k−NN(k−N)

Simplify each fraction:1k−N + 1N

Now it is a lot easier to solve. We can integrate each term separately, like this:

Our full equation is now:∫1k−NdN + ∫1NdN = ∫ r dt

Integrate:−ln(k−N) + ln(N) = rt + C

(Why did that become minus ln(k−N)? Because we are integrating with respect to N.)

Step 3 Simplify:

Negative of all terms:ln(k−N) − ln(N) = −rt − C

Combine ln():ln((k−N)/N) = −rt − C

Now take exponents on both sides:(k−N)/N = e^−rt−C

Separate the powers of e:(k−N)/N = e^−rt e^−C

e^−C is a constant, we can replace it with A:(k−N)/N = Ae^−rt

We are getting close! Just a little more algebra to get N on its own:

Separate the fraction terms:(k/N)−1 = Ae^−rt

Add 1 to both sides:k/N = 1 + Ae^−rt

Divide both by k:1/N = (1 + Ae^−rt)/k

Reciprocal of both sides:N = k/(1 + Ae^−rt)

And we have our solution:

N = k1 + Ae^−rt

Here is an example, the graph of 401 + 5e^−2t

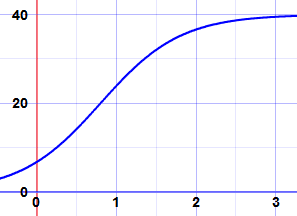
verhulst
It starts rising exponentially,
then flattens out as it reaches k=40