Solving SSA Triangles

"SSA" means "Side, Side, Angle"

"SSA" is when we know two sides and an angle that is not the angle between the sides.

To solve an SSA triangle

use The Law of Sines first to calculate one of the other two angles;
then use the three angles add to 180° to find the other angle;
finally use The Law of Sines again to find the unknown side.

Example 1

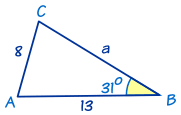
trig SSA example

In this triangle we know

angle B = 31°
b = 8
and c = 13

In this case, we can use The Law of Sines first to find angle C:

sin(C)/c = sin(B)/b

sin(C)/13 = sin(31°)/8

sin(C) = (13×sin(31°))/8

sin(C) = 0.8369...

C = sin⁻¹(0.8369...)

C = 56.818...°

C = 56.8° to one decimal place (*see below)

Next, we can use the three angles add to 180° to find angle A:

A = 180° − 31° − 56.818...°

A = 92.181...° = 92.2° to one decimal place

Now we can use The Law of Sines again to find a:

a/sin(A) = b/sin(B)

a/sin(92.181...°) = 8/sin(31°)

Notice that we didn't use A = 92.2°, that angle is rounded to 1 decimal place. It's much better to use the unrounded number 92.181...° which should still be on our calculator from the last calculation.

a = (sin(92.181...°) × 8)/sin(31°)

a = 15.52 to 2 decimal places

So, we have completely solved the triangle ...

... or have we?

* Back when we calculated:

C = sin⁻¹(0.8369...)
C = 56.818...°

We didn't think that sin⁻¹(0.8369...) might have two answers (see Law of Sines)

The other answer for C is 180° − 56.818...°

Here you can see why we have two possible answers:

trig SSA example

By swinging side "8" left and right we can
join up with side "a" in two possible locations.

So let's go back and continue our example:

The other possible angle is:

C = 180° − 56.818...°

C = 123.2° to one decimal place

With a new value for C we will have new values for angle A and side a

Use "the three angles add to 180°" to find angle A:

A = 180° − 31° − 123.181...°

A = 25.818...°

A = 25.8° to one decimal place

Now we can use The Law of Sines again to find a:

a/sin(A) = b/sin(B)

a/sin(25.818...°) = 8/sin(31°)

a = (sin(25.818...°)×8)/sin(31°)

a = 6.76 to 2 decimal places

So the two sets of answers are:

C = 56.8°, A = 92.2°, a = 15.52

C = 123.2°, A = 25.8°, a = 6.76

Example 2

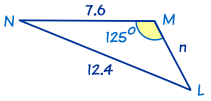
trig SSA example

This is also an SSA triangle.

In this triangle we know angle M = 125°, m = 12.4 and l = 7.6

We will use The Law of Sines to find angle L first:

sin(L)/l = sin(M)/m

sin(L)/7.6 = sin(125°)/12.4

sin(L) = (7.6×sin(125°))/12.4

sin(L) = 0.5020...

L = 30.136...°

L = 30.1° to one decimal place

Next, we will use "the three angles add to 180°" to find angle N:

N = 180° − 125° − 30.136...°

N = 24.863...°

N = 24.9° to one decimal place

Now we will use The Law of Sines again to find n:

n/sin(N) = m/sin(M)

n/sin(24.863...°) = 12.4/sin(125°)

n = (sin(24.863...°)×12.4)/sin(125°)

n = 6.36 to 2 decimal places

Note there is only one answer in this case. The "12.4" line only joins up one place.

The other possible answer for L is 149.9°. But that is impossible because we already have M = 125° and a triangle can't have two angles greater than 90°.

Conclusion:

When solving a "Side, Side, Angle" triangle we need to
check if there could be another possible answer!